平衡树和红黑树
平衡树和红黑树是计算机科学中用于组织数据的重要数据结构,它们各自具有特定的特性和应用场景。
平衡树
平衡树是一类动态的数据结构,其最大的特点是能够维护修改操作(如插入、删除)、前驱后继操作、查找数k的排名、查找第k大等功能,同时保持树的平衡状态,以确保这些操作的高效性。平衡树通过特定的算法(如旋转操作)在插入或删除节点后重新调整树的结构,以保持树的平衡,从而使得树的高度保持在较低的水平,进而保证操作的高效性。
红黑树
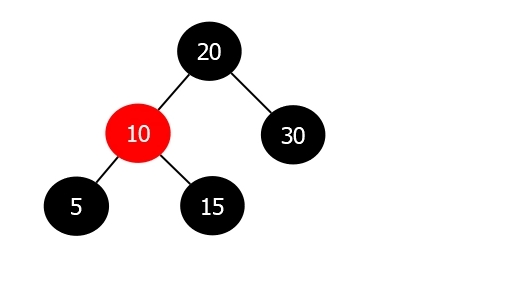
红黑树是一种自平衡的二叉搜索树(Binary Search Tree),它在计算机科学中用于组织数据,如数字的块。红黑树是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees),后来被Guibas和Robert Sedgewick修改为如今的“红黑树”。红黑树是一种特化的AVL树(平衡二叉树),它在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。
红黑树的特点包括:
节点颜色:每个节点都包含一个额外的存储位来表示节点的颜色,可以是红色或黑色。
自平衡特性:红黑树在插入和删除节点时,通过自我调整来保持树的平衡。这个平衡的过程是通过调整节点的颜色和树的结构来实现的。
节点属性:
- 节点或是黑色或是红色。
- 根节点是黑色。
- 所有叶子节点(NIL节点,空节点)都是黑色。
- 如果一个节点是红色,那么它的两个子节点都是黑色。
- 从任意节点到其每个叶子节点的路径都包含相同数目的黑色节点。
红黑树的这些特点使得它在最坏情况下的运行时间也非常良好,可以在O(log n)时间内完成查找、插入和删除操作,这里的n是树中元素的数目。
应用场景
由于红黑树的高效性和自平衡特性,它被广泛用于各种需要高效插入、删除和查找操作的场景,如:
- 数据库索引:红黑树可以用于实现数据库的索引结构,提高数据库的查询效率。
- C++的STL库:C++标准模板库(STL)中的map和set容器底层通常使用红黑树来实现,以支持高效的查找、插入和删除操作。
- 平衡查找树的需求:红黑树可以作为平衡查找树的一种实现方式,用于快速查找和有序遍历数据。
综上所述,平衡树和红黑树都是计算机科学中重要的数据结构,它们通过保持树的平衡状态来提高各种操作的高效性。红黑树作为平衡树的一种具体实现方式,在实际应用中具有广泛的应用场景。



